構造化・素子化・微細化で得られること
一口に構造化と言っても大変幅が広いものです.ごく簡単なものとしては,比較的電気抵抗率の高い物質の抵抗率を測定する際,ホールバーと呼ばれる4端子構造に加工することが挙げられます.一般に簡易法に比べて信頼度の高いデータを得ることができます.
試料の微細化の利点の一つが,純良な試料を得る可能性があることです.大きく純良な単結晶が得にくい場合,微小試料により単結晶単一ドメインの電気伝導を測定したり,不均一試料から,パラメーターの異なる複数試料についての情報が得られる可能性があります.
素子化でわかりやすいのは,物質科学で「電場ドープ」という不思議な呼称で呼ばれている手法でしょう.代表的手法としては,試料表面を絶縁薄膜,更にその上の金属薄膜(ゲート電極)で覆い,このゲート電極への電圧によって表面付近に強い電場を印加して電荷キャリア密度を制御するものがあります.
このように,バルク試料の加工等により,基本的物性以外に非平衡物性や様々な機能性の検証を行う可能性が広がります.このページでは,ごく基本的な微細化に伴う性質変化について紹介します.
当然ながら,新しく発見され新奇な性質を持つ物質の微細構造や素子は,また異なる知見をもたらしてくれるに違いなく,本ラボにおいて物質科学とナノ科学の相乗効果により,新たな量子効果が見いだされることを期待しています.
微細化と低次元化
系の次元はどのような現象,自由度に着目するか,で異なります.微細化による量子的な閉じ込め効果を考える場合,通常は閉じ込めサイズは閉じ込め対象の粒子のド・ブロイ波長と同程度以下である必要があります.電子系の場合はフェルミ波長になります.多くの金属では,フェルミ波長は極めて短く,ほぼ格子定数まで小さくしなければならないことになります. しかし,特に後述の量子ドットの場合は必ずしもそうではありません. 以下,主に電子系で考えることにしますが,他の粒子系でも類似現象が生じます.
量子化による低次元化
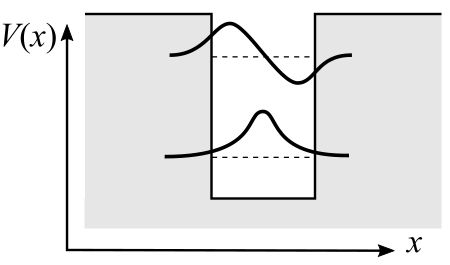
図のように,矩形にへこんだポテンシャルが初等量子力学でおなじみの量子井戸ポテンシャルですね. ポテンシャルの底から上端までにいくつか離散準位,空間的には局在した状態ができます.
実際には,薄膜化や異種物質の接合(ヘテロ接合)で挟むことで,薄膜や接合に垂直方向の運動に,これに類似のポテンシャルを導入することが行われます. すると,電子系の運動自由度は,この方向の波動関数に局在波動関数を選べば1次元下がって2次元となります. このような構造を,ポテンシャルの呼称と同じく量子井戸構造と呼んでいます.
2次元系に更に量子井戸的なポテンシャルにより閉じ込めを行うと,系の次元は1次元になります.このような1次元系を量子細線と呼びます. 1次元系に更に量子井戸ポテンシャルを加えて局在化することで,電子の運動自由度はゼロで,0次元系が実現します.これが量子ドットと呼ばれるものです.
量子ドットになると,閉じ込めポテンシャル障壁が十分高ければ,量子化によって固有エネルギーが大きく変化し,フェルミ準位付近での離散準位間隔が温度揺らぎなどに比べて十分大きくなると,バルクでは金属の物質も性質が大きく変化し,バルクのフェルミ波長よりもはるかに大きな構造でも量子ドットとして扱うことが必要になります. このような金属由来の量子ドットは,金属超微粒子として古くから研究され,久保亮五による久保効果は,これを舞台にした物理現象として有名です. 教会のステンドグラスの色など,古くからある工芸技術などもこのような物理を意識せずに使用していたものです. 更にサイズが小さくなり,1ドットあたりの原子数がカウントできる程度になると,クラスターと呼ばれるようになり,表面の影響が大きく結晶形や格子振動も大きく変化します.
現象の特徴的長さと低次元化
運動の量子化を用いた低次元化に対して,もっと大きな構造でも実効的な低次元化が生じる場合があります. 電気伝導で考えると,キャリアの平均自由行程よりも狭い閉じ込め構造を導入すると,波動関数は量子化していなくても電荷の動きの次元は下がるため,低次元伝導体として扱える場合があります. このような特徴的な長さは,対象とする物理現象によって様々に変化します.現象の種類や,温度や磁場,圧力など環境のパラメーターにより次元がクロスオーバーすることもあります.
物性研究者が良く知っている例としては,超伝導が挙げられます.超伝導現象には様々な長さのパラメーターが存在し,考えている物質のサイズがこれらと同等以下になると,超伝導の性質が大きく変化します.
低次元構造から人工構造へ
次元を下げて作り出した井戸,細線,ドットなどを,今度は組み合わせて新しい構造を作り出すことも考えられます.電子系では,江崎とTsuによって考えられた超格子がその始まりと言ってよいでしょう.超格子では,離散的な空間並進対称性が回復されるため,局在化した状態が結合して新しいエネルギーバンド(ミニバンド)が形成されます.

GaAs/AlAs超格子の断面透過電子顕微鏡写真
電子系ばかりではなく,他の粒子や準粒子についても同様です. 例えばフォノンについて,固体内に構造を作り,様々な特異なモードを作り出すことができます. 光子についても同じで,固体中に導波路を作ったり,フォトニック結晶,その中の「格子欠陥」による光子の量子ドット,そしてメタマテリアル概念の導入なども行われています.
更に,例えば誘電率に強い分布を持たせることで電場の2次元化を図ることもできます. これによって,電荷の間に超伝導薄膜の量子化磁束の間と同型の有効な相互作用が生まれ,BKT転移など様々な現象が現れることが報告されています.
素子化で調べる諸現象
構造化と素子化はほぼ同義と言っても良いと思いますが,「素子」(device)と言うと,やはり電子回路の中で何らかの機能を発揮するものを考えます.すなわち,「端子」を持ち,これを電子回路につなぎこむことで回路と素子で相互にパラメーターを制御し合うことで,信号処理や電力の伝達を行うものです.
物質パラメーターの制御
物質パラメーターの制御,具体的にはキャリア濃度の制御によって機能を生み出す素子の代表が電界効果トランジスタ (Field Effect Transistor, FET)です.このような電場によるキャリア濃度制御が,物質科学においても様々に使用されるようになってきました.
代表的手法が,試料表面に絶縁体薄膜を形成し,金属のゲート電極を付けて電場を印加するものです. 良く使用されるようになった一因は,原子層堆積法 (atomic layer deposition, ALD)の開発により,良質な絶縁体薄膜が比較的平坦性の悪い表面にも堆積できるようになったことです.
これと並んで,電解液を用いる方法も使用されます.試料表面を電解液に触れさせ,試料-電解液に電圧を加えると,電解液面に二重層ができて試料に強い電場が印加されキャリア濃度を大きく変えることができます.MoS2において,この手法により超伝導が誘起される現象が見つかったのは物性研究者のよく知るところです.
非平衡現象

池の中の状態を,魚を放流し(非平衡状態)これがどのようにして捕獲されるかを見て調べる(伝導現象).
上の図は,Zagoskinの多体問題の教科書(A. Zagoskin, "Quantum Theory of Many-Body Systems" (Springer, 1998))にあった,「伝導現象にどうして多体効果が反映されるか」ということを説明するイラストを,少し真似して描いたものです. 池の中(赤い線の下)には沢山の魚がいて色々なことをして(相互作用)います.何をしているのか,どれくらい混み合っているのか,調べるための方法として,魚を放流して,魚群に擾乱を与えて平衡状態からずらし,別の地点でどれくらい魚が捕獲されるかを調べるというもので,非平衡現象を通して多体効果を検知する手法を表しています. このように,電気伝導やスピン伝導など,非平衡現象は,もちろんそれ自身として大変興味深いばかりでなく,平衡状態の性質を知る上でも大変有用です.
非平衡現象を用いた素子の代表は,Shockleyが発明した接合型トランジスタで,半導体への少数キャリア注入現象が電流増幅機能の中心原理になっていました.発光ダイオード,太陽電池,みなこの現象によって機能を発揮しています.現在の固体物理学研究においては,このような界面を通した注入現象は数多く知られています. 例えば,超伝導-常伝導接合においては,条件によってはクーパー対(あるいは超伝導ギャップ)の滲み出しによる近接効果が生じます. また条件によっては,アンドレーフ反射と呼ばれるクーパー対が電子-正孔対に転写され超伝導コヒーレンスが伝播する現象も生じます.
平衡キャリア濃度が低い半導体へのキャリア注入が劇的効果をもたらすように,平衡状態では平均で内部磁気モーメントを持たない常磁性金属へのスピン注入は大きな効果を引き起こします.スピントロニクスの発祥をもたらした巨大磁気抵抗効果 (giant magnetoresistance, GMR) も常磁性体-強磁性体の超格子構造において最初に発現したものです. 物質の構造化,素子化は,このような現象の研究に極めて有効です.
